Landscapes, Test problems for optimization

Function	Definition	Heat Map	Surface
Ackley Function	\( f(\mathbf {x} )= -20 \exp\left[-0.2\sqrt{ \frac{1}{n}\sum _{i=1}^n{ x_i^2 } } \right] \\ - \exp\left[ \frac{1}{n}\sum _{i=1}^n{ cos(2 \pi x_i) } \right] + 20 + e \) Global minimum at \( \mathbf{x} = 0 \)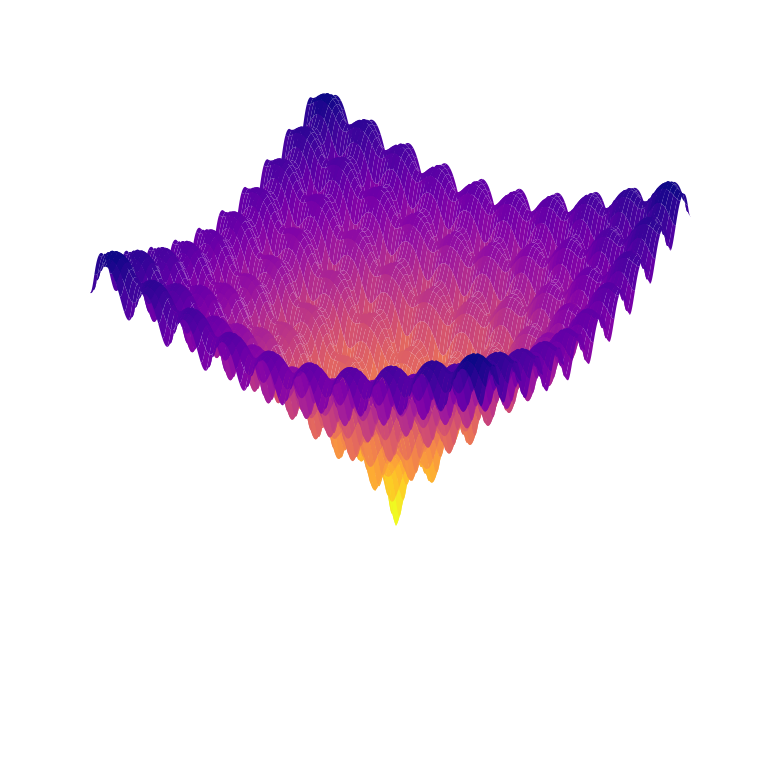
Rastrigin Function	\( f(\mathbf {x} )=10n+\sum _{i=1}^{n}\left[x_{i}^{2}-10\cos(2\pi x_{i})\right] \) Global minimum at \( \mathbf{x} = 0 \)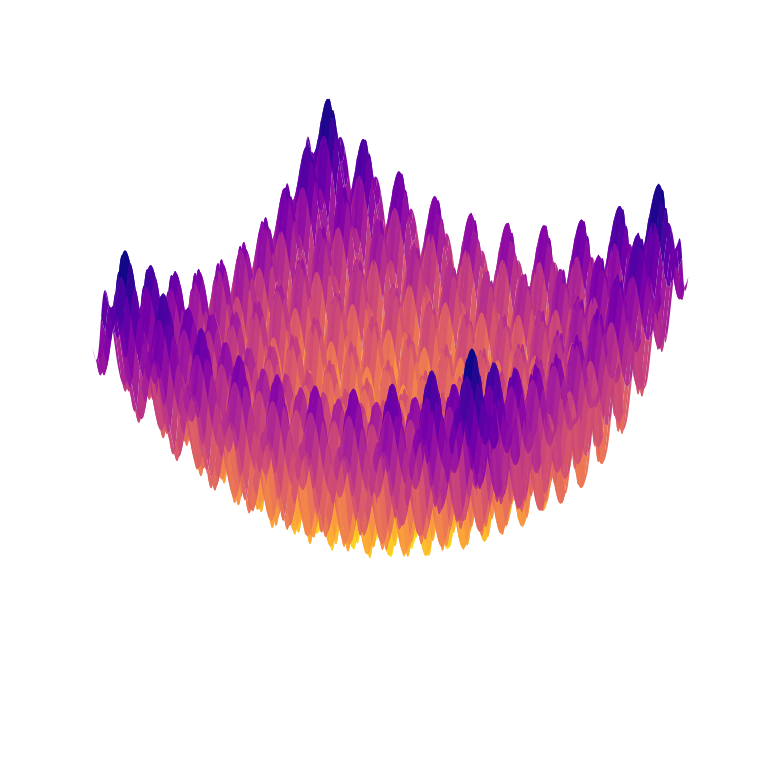
Dropwave Function	\( f(\mathbf {x} )= -\frac{1 + \cos(12\sqrt{\sum_{i=1}^{n}x_{i}^{2})}}{0.5\left[\sum_{i=1}^{n}x_{i}^{2}\right] + 2} \) Global minimum at \( \mathbf{x} = 0 \)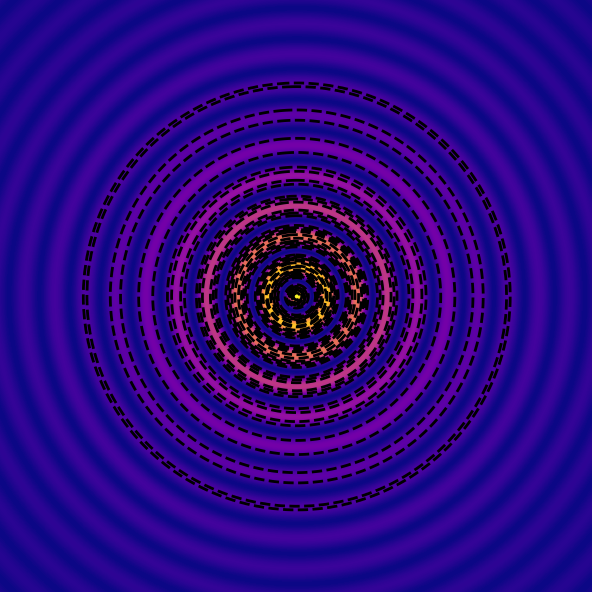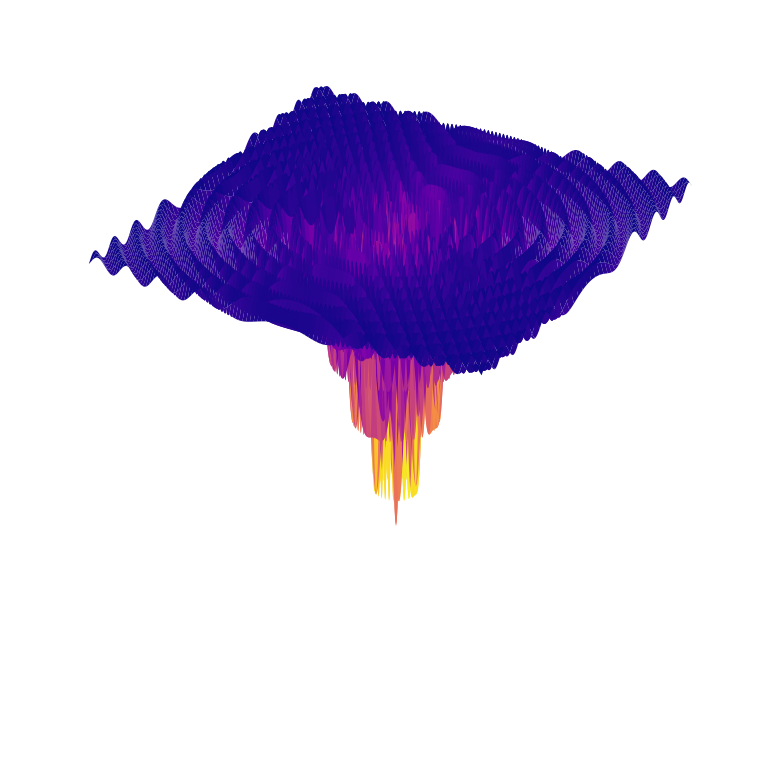
Griewank Function	\( f(\mathbf {x} )=1 + \sum _{i=1}^{n}\frac{x_{i}^{2}}{4000} - \prod _{i=1}^{n}\cos{\frac{x_{i}}{\sqrt{i}}} \) Global minimum at \( \mathbf{x} = 0 \)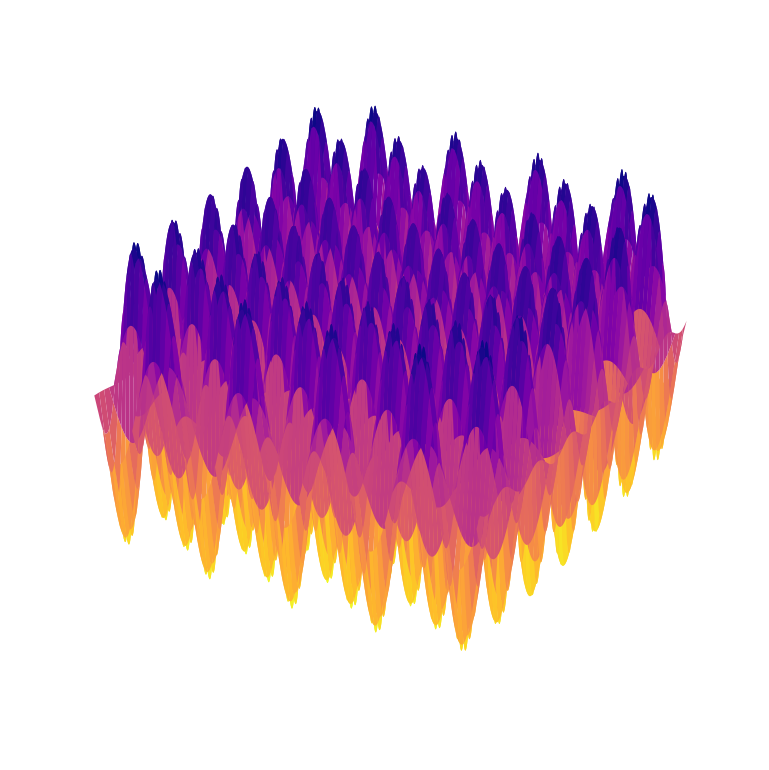
Sphere Function	\( f(\mathbf {x} )=\sum _{i=1}^{n}x_{i}^{2} \) Global minimum at \( \mathbf{x} = 0 \)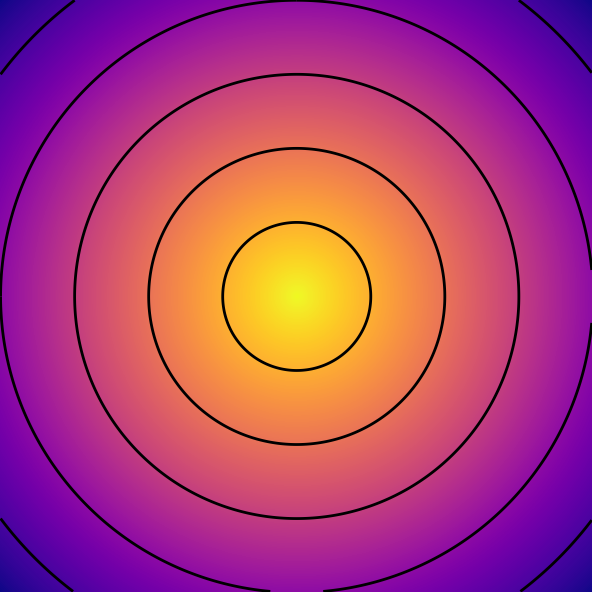
Rosenbrock Function	\( f({\mathbf {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}\right] \) Global minimum at \( \mathbf{x} = \mathbf{1} \)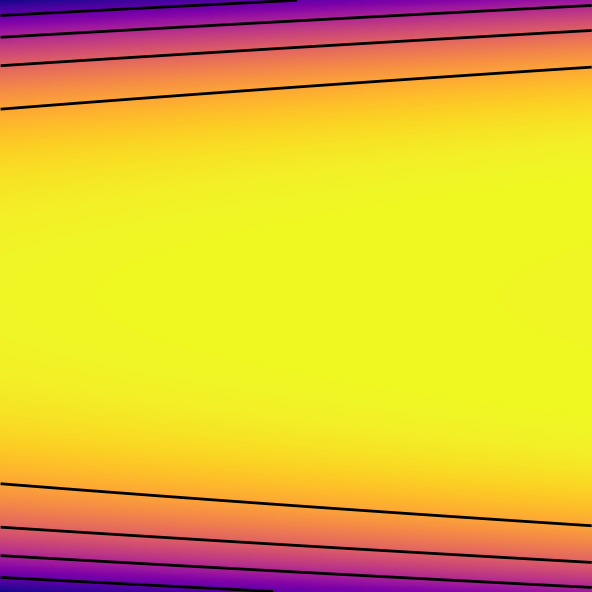

References

• https://www.sfu.ca/~ssurjano/griewank.html
• https://www.sfu.ca/~ssurjano/drop.html