In this example we design an optimizer in Dena step by step and then we will see how to execute it using Zagros runtime. But first, make sure you have read Using RockyML with CMake. Here is a blank template for beginning:

#include <mpi.h>
#include <rocky/zagros/benchmark.h>
#include <rocky/zagros/flow.h>
 
using namespace rocky::zagros;
using namespace rocky::zagros::dena;
 
int main(int argc, char* argv[]){
    MPI_Init(&argc, &argv);
    
    // our code
 
    MPI_Finalize();
    return 0;
}

Problem Definition

We are going to minimize the Rastrigin function defined as:

\[ f(\mathbf{x})=10n+\sum _{i=1}^{n}\left[x_{i}^{2}-10\cos(2\pi x_{i})\right] \]

On the domain \( \mathbf{x} \in \left[ -5.12,5.12 \right]^{n} \) where \( n=100 \). Before everything, let's know our objective function better. Rastrigin is a famous function in optimization literature. If we plot it for \( n=2 \) we have:

Heat Map	Surface

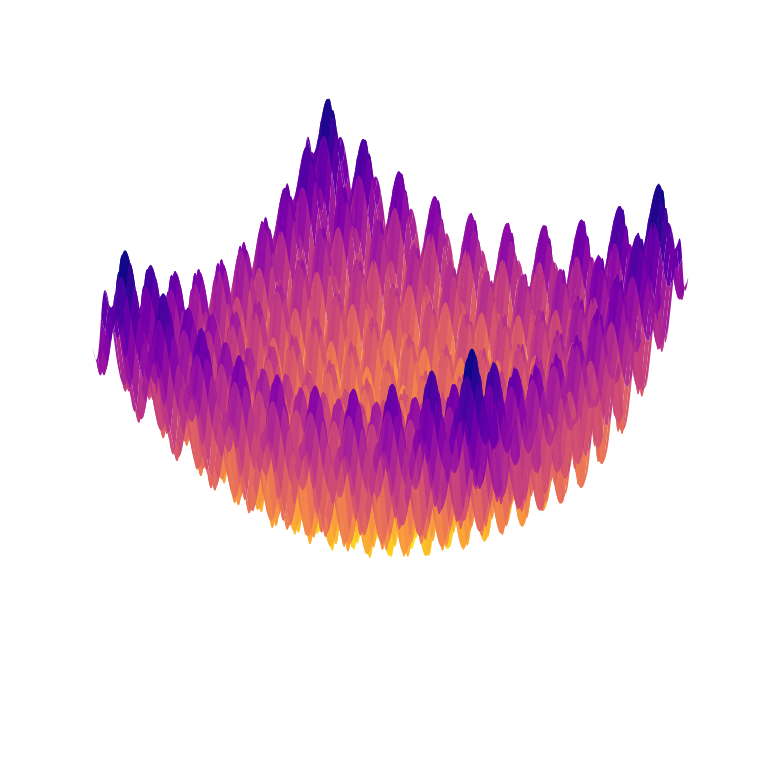As you can see it has so many local minimums. In fact, as the dimension increases, the number of local minimums increases exponentially! On the domain of \( \left[ -5.12,5.12 \right]^{100} \) it has \( 11^{100} \) local minimums 😱. The global minimum is located at \( \mathbf{x} = 0 \). Since Rastrigin is a famous function, it's available in the set of test functions in Zagros

// objective dimension
const int n = 100;
// define rastrigin function
benchmark::rastrigin<float> objective(n);

A simple optimizer

Next we need to describe our optimizer. Dena is a language for specifying optimization algorithms. Using Dena, you can focus on the optimization procedure and leave the execution to Zagros runtime. There are many search methods for black-box optimization, you can freely combine them in various ways. To illustrate how this works, we begin with a very simple optimizer then slightly evolve it to a complex algorithm for optimization.

In Zagros, a solution container holds a set of potential solutions to an optimization problem. An optimizer essentially acts on the containers to improve their solutions gradually. Thus the first step is to create a solution container:

auto optimizer = container::create("A");

The above code, simply create a container A containing a solution. So far we have only a single solution. We can initialize it now:

auto optimizer = container::create("A") >> init::uniform("A");

This will initialize the solution using a uniform distribution. container::create and init::uniform are called optimization flow. A flow is a sequence of operations in Zagros optimizers. you can combine flows using operator >> to create more complex flows. Dena supports various flows each one for a different purpose. After initializing we can use search strategies to improve the solution. A simple strategy might be adding a gaussian noise to the solution and keep the changes if it causes any improvement:

auto optimizer = container::create("A") 
                >> init::uniform("A")
                >> mutate::gaussian("A");

mutate::gaussian adds a gaussian noise to the solutions and update them if the noise improves them. Of course we can control the number of affected dimensions and parameters of the noise if we like. By repeating this procedure we obtain a simple hill climbing. To repeat a flow you can use run::n_times:

auto optimizer = container::create("A")
                >> init::uniform("A") 
                >> run::n_times(500,
                      mutate::gaussian("A")
                );

run::n_times(100, f) will run a flow f for 100 times. let's see the performance of our simple optimizer. log::local::best is a utility for recording best solution in a container. Using log::local::best we can store the best found solution in each time step in a local file. Dena also provides utilities for logging on a remote tracker like Comet. To specify the output of logging we should create a local_log_handler object:

local_log_handler log_handler("result.csv");

The result will be stored in a file called result.csv.

auto optimizer = container::create("A")
                >> init::uniform("A") 
                >> run::n_times(500,
                      mutate::gaussian("A")
                      >> log::local::best("A", log_handler)
                );

After designing the optimizer we should execute it using Zagros runtime:

// create a runtime for executing the optimizer 
zagros::basic_runtime<float, dim> runtime(&problem);
runtime.run(optimizer);

So the full example would be:

#include <mpi.h>
#include <rocky/zagros/benchmark.h>
#include <rocky/zagros/flow.h>
 
using namespace rocky::zagros;
using namespace rocky::zagros::dena;
 
int main(int argc, char* argv[]){
    MPI_Init(&argc, &argv);
    
    // define the optimization problem
    const int dim = 100;
    benchmark::rastrigin<float> problem(dim);
 
    // recording the result of optimization
    local_log_handler log_handler("result.csv");
 
    // define the optimizer
    auto optimizer = container::create("A", 300)
                    >> init::uniform("A") 
                    >> run::n_times(500,
                            mutate::gaussian("A")
                            >> log::local::best("A", log_handler)
                        );
 
    // create a runtime for executing the optimizer 
    basic_runtime<float, dim> runtime(&problem);
    runtime.run(optimizer);
 
    MPI_Finalize();
    return 0;
}

After compiling the program, we should run it using MPI:

mpirun -np 1 ./app

And if we plot the results stored in this file, we have:

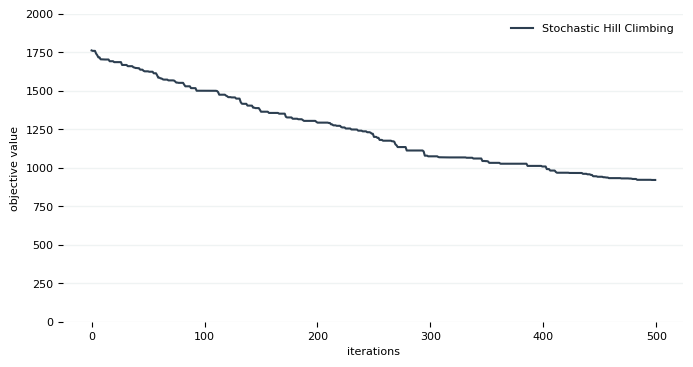
Hmmm, not so bad. It seems we trapped in one of those local minimums. Perhaps we should run this algorithms multiple times. So why not run them in parallel?

A parallel optimizer

In the previous example container::create("A") created a single solution (particle) for us. To construct a parallel variant of stochastic hill climbing we can simply create a container with more solutions.

container::create("A", 300)

So now we have:

auto optimizer = container::create("A", 300)
                >> init::uniform("A") 
                >> run::n_times(500,
                      mutate::gaussian("A")
                      >> log::local::best("A", log_handler)
                );

Note if your CPU supports multi-threading, Zagros will exectue the optimization in parallel. But make sure you assign enough processing elements to the process when using mpirun. If we plot the result of this version:

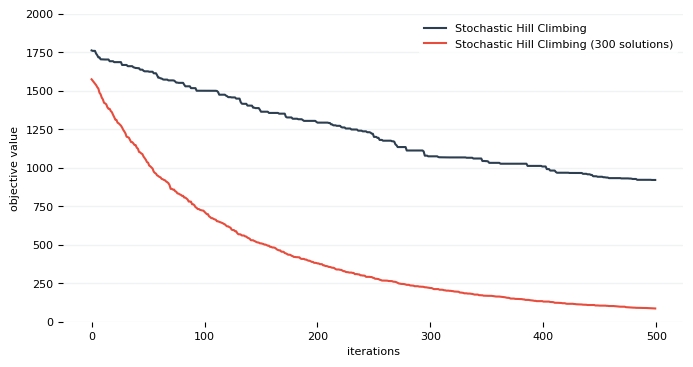
Some of population-based optimiztion algorithms are also available in Dena that can be applied on a solution container. For example you can use Differential Evolution with crossover::differential_evolution. But suppose instead of running it every time, we want to execute with a certain probability. To do so we can simply use run::with_probability:

auto optimizer = container::create("A", 300)
                >> init::uniform("A") 
                >> run::n_times(500,
                      mutate::gaussian("A")
                      >> run::with_probability(0.2,
                          crossover::differential_evolution("A")
                      )
                      >> log::local::best("A", log_handler)
                );

And not surprisingly a little more improvement:

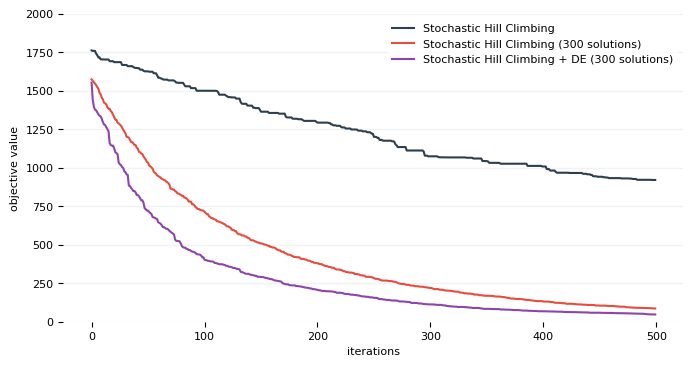
Why not make it even more complicated 🤡 ?

auto optimizer = container::create("A", 300)
                >> init::uniform("A") 
                >> run::n_times(500,
                      mutate::gaussian("A")
                      >> run::with_probability(0.2,
                          crossover::differential_evolution("A")
                      )
                      >> run::every_n_steps(4, 
                          eda::mvn::full_cov("A")
                      )
                      >> log::local::best("A", log_handler)
                );

run::every_n_steps as its name suggests, runs a flow every n steps. eda::mvn::full_cov is a variant of an evolution strategies called EDA (Estimation of Distribution Algorithm). And again 🙄 if we plot the result:

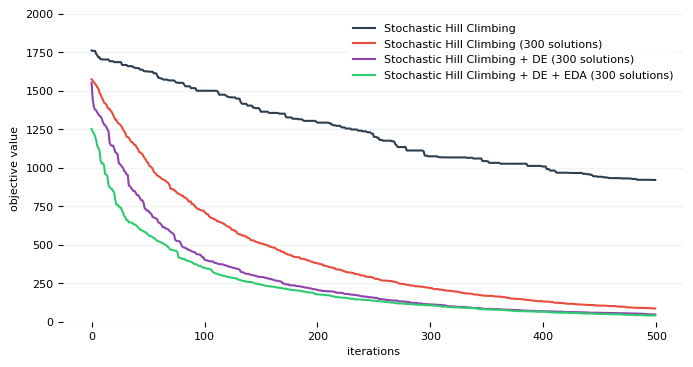
We should stop since there is no honor in just stacking a few search algorithm on top of each other. But the point is, using Dena we can freely combine various algorithms in a unified way. The search strategies in Dena have parallel implementation so we should expect a speedup on CPUs with multiple cores:

Conclusion

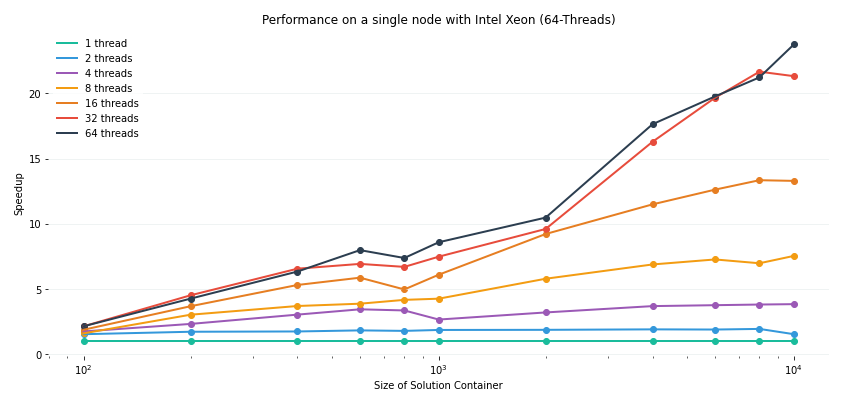
So far we have designed a single node optimizer. Zagros also provides facilities for distributed optimization like solution propagation in addition to other utilities for using optimizers on large-scale problems which will be covered in another tutorial.